Trie

Trie is a popular data structure to store and process strings, that sometimes appears in the interview questions. In this section, we will learn what trie is, how to write one, and how it can be used.

Trie structure

Trie is a rooted tree that stores a set of strings. Each string starts at the root, and each edge in the tree represents a single character.

For example, the word candle will look like this:

Words that share the same prefix (beginning of the word) will also share some trie edges and nodes. For example, trie storing words candle and canary will look like this:

In the example above, you can already see how trie can be useful. We store both words candle and canary, but save on the memory by sharing the common elements.

Let's say we add the word can to the set. It will not require any additional edges or nodes, but now we will need to somehow know where the word in the trie ends. We can mark the end of a word in the trie with the blue colored nodes. The following trie stores words candle, canary, and can:

If we add a word that doesn't share any prefix with the words already in the trie, we will have a new branch from the root node. Here is the previous trie with the word lion added:

Coding trie

Trie may look great in theory, but how to actually implement it? Turns out, it is pretty simple.

All we really need is a class for a trie node. In the node, we will keep edges starting there (we will keep them in the map with character as the key and the next node as the value), and a boolean marking the end of the word.

class TrieNode {
    Map<Character, TrieNode> edges;
    boolean isWordEnd;
    
    TrieNode() {
        this.edges = new HashMap<>();
        this.isWordEnd = false;
    }
}

Trie itself can be now represented simply as its root node:

TrieNode root = new TrieNode();

Inserting a word in the trie is pretty simple now. We start from the root, iterate over the characters of the new word, and move along the nodes and edges, creating them when needed. Here is the full code:

public void insert(TrieNode root, String word) {
    TrieNode currentNode = root;
    for (char c : word.toCharArray()) {
        if (!currentNode.edges.containsKey(c)) {
            currentNode.edges.put(c, new TrieNode());
        }
        currentNode = currentNode.edges.get(c);
    }
    currentNode.isWordEnd = true;
}

Searching if some word exists in the trie is pretty simple too. Again, we start from the root, iterate over the characters of the new word, and move along nodes and edges of the trie. This time, though, we don't create anything – if we try to move along the edge that doesn't exist, we simply return false. In the end, we also need to check if a word ends in the node we are currently in.

public boolean search(TrieNode root, String word) {
    TrieNode currentNode = root;
    for (char c : word.toCharArray()) {
        if (!currentNode.edges.containsKey(c)) {
            return false;
        }
        currentNode = currentNode.edges.get(c);
    }
    return currentNode.isWordEnd;
}

You can also wrap all the code above in the Trie class if you want, to create a completely separate trie structure:

class Trie {
    private class TrieNode {...}

    private TrieNode root;

    public Trie() {
        this.root = new TrieNode();
    }

    public void insert(String word) {
        TrieNode currentNode = root;
        ...
    }

    public boolean search(String word) {
        TrieNode currentNode = root;
        ...
    }
}

Trie trie = new Trie();
...

Trie applications

So, how can we use trie? There are several applications.

First, a trie is a convenient way to store a set of strings. Inserting a string of length L in the trie takes O(L) time, which is optimal (you need to access all characters in the string at least once to store it, after all). We can also check if the trie contains a string of length L in O(L) time, which is also optimal.

Trie also has some memory advantages. When several strings have a common prefix, trie reuses some nodes and edges for all of them, thus saving space. Of course, in the worst case, when all stored strings start with a different letter, there are no memory optimizations.

Trie is also relatively easy to code. The disadvantage here though is that trie is missing in the standard libraries of both Java and C++ (as well as many other languages), so you will need to code it yourself.

Trie is also very useful when working with prefixes. Because words with the same prefixes share nodes and edges in the trie, we can efficiently answer the following questions with the trie (perhaps with some modifications):

• Are there any words in the trie that start with the prefix P?
• How many words in the trie start with the prefix P?
• What are all the words in the trie that start with the prefix P?

Because of this, data structures similar to a trie are used in many real-life applications. Google search autocomplete is a great example of this. When you type the beginning of your search query, it looks for the possible ways to continue it that start with the typed prefix:

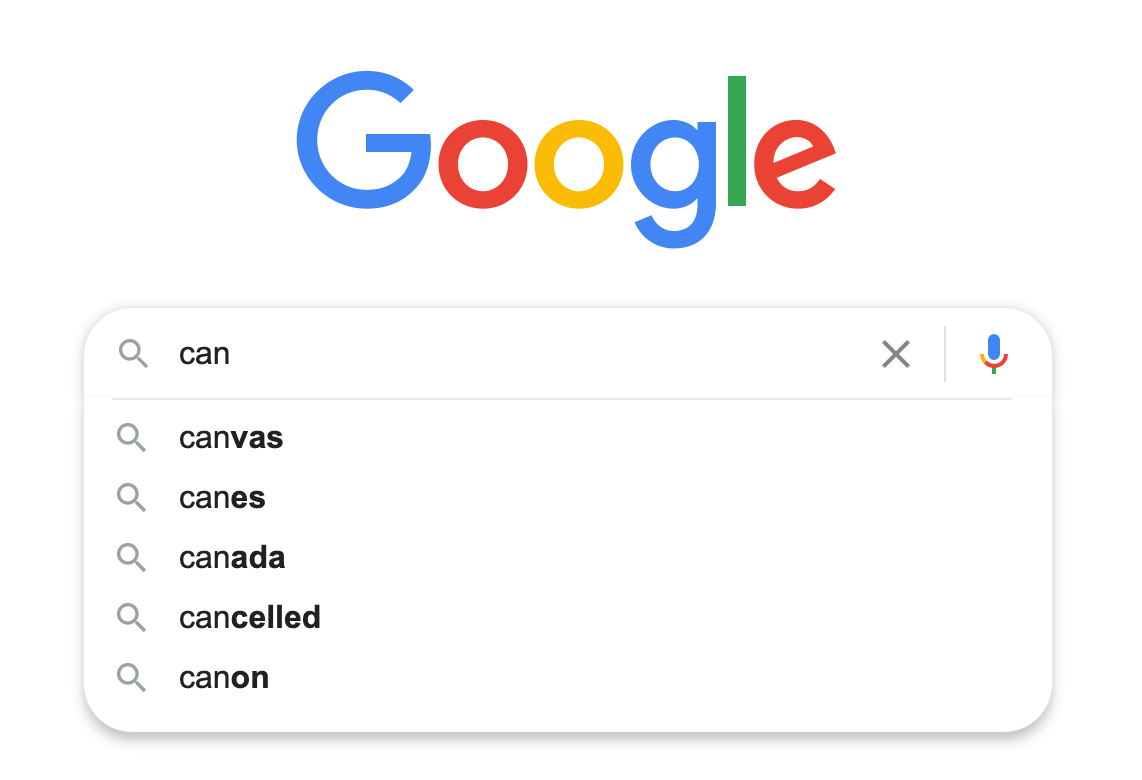
You can try to figure out yourself how you can use trie to answer three prefix related questions above – it is a good exercise. We will also cover this when we will study trie interview problems below. In general, when the interview question has something to do with the string prefixes, you can try to see if you can use trie there.

Trie interview problems

Now, let's solve some trie related interview questions.

The following problem is a great place for practice, because it literally asks you to just implement trie. Can you do it without looking at the code above?

The following problem nicely uses trie, and requires some additional thinking. Can you solve it?

In the following problem, you will need some modifications of the trie structure. It is a good way to practice handling additional operations with trie.

The following problem is a tough one. Before you start it, make sure you have read an article about backtracking and have solved Word Search problem. It is a good classic problem though, and often appears on the interviews as a follow up to the Word Search problem:

More trie problems

Here are some more good trie problems to practice: